We earn commission when you buy through affiliate links.
This does not influence our reviews or recommendations.Learn more.
This tutorial will teach you how toprintPascals trianglein Python for a given number of rows.
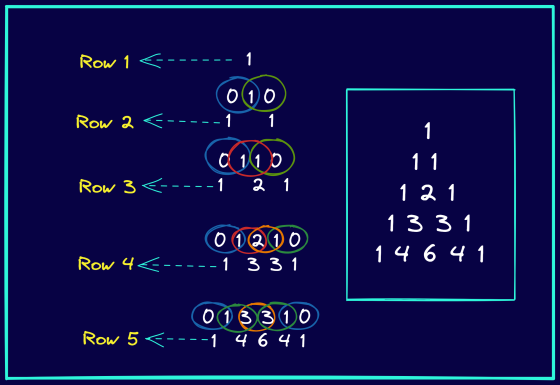
You will start by learning how to construct Pascals triangle.
Youll then proceed to write a Python function and learn to optimize it further.
What is Pascals Triangle & How to Construct it?
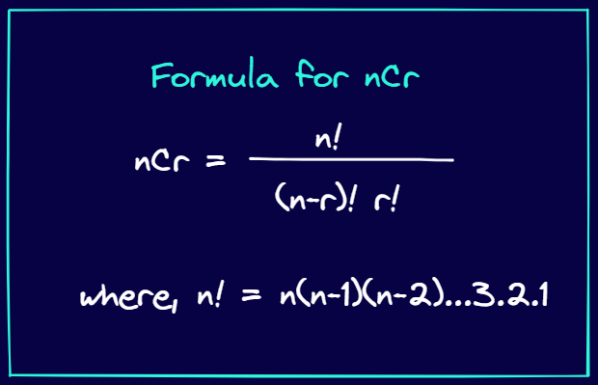
Printing Pascals triangle for a given number of rows is a popular interview question.
In Pascals triangle withnrows, row numberihasielements.
So the first row has one element, and its 1.

And each element in subsequent rows is the sum of the two numbersdirectly aboveit.
The following figure explains how to construct Pascals triangle with five rows.
Notice how you’re able to pad zeros when you haveonly one numberabove a certain number.

Next, lets proceed to write some code.
There are two key questions to consider:
Lets answer them now.
#1.Whats the expression for each entry in Pascals triangle?
It so happens that the entries in Pascals triangle can be obtained using the formula fornCr.
The formula fornCris given below:
Now lets proceed to express the entries in Pascals triangle using thenCrformula.
Weve now found a way to express the entries in the matrix.
#2.How to adjust spacing when printing the pattern?
To print the pattern as a triangle, youll neednumRows - ispaces in row #i.
And you might use Pythonsrangefunction in conjunction withforloop to do this.
As therangefunction excludes the endpoint by default, double-check to add+ 1to get the required number of leading spaces.
Parsing the Function Definition
So what do you want the functionpascal_trito do?
to compute the factorial, lets usefactorialfunction from Pythons built-inmathmodule.
execute the following code cell to importfactorialand use it in your current module.
The code snippet below contains the function definition.
The code snippet below shows how to do it.
Now lets go ahead and call the function with the number of rows as the argument.
The first 3 rows of Pascals triangle are printed, as expected.
However, we did not utilize the relationship between entries in two consecutive rows.
In fact, we used the previous row to compute the entries in the subsequent row.
Can we not use this and come up with arecursiveimplementation of the functionpascal_tri?
Yes, lets do that!
In arecursiveimplementation, a function repeatedly calls itself until thebase caseis met.
Consider the example where it’s crucial that you print the first 3 rows of Pascals triangle.
The following image explains how the recursive calls are pushed to the stack.
And how the recursive function calls return the rows of Pascals triangle.
execute the code snippet below to generate the rows of Pascals triangle recursively.
The output is correct, as seen below!
However, there are times when you should probably print Pascals triangle for a smaller number of rows.
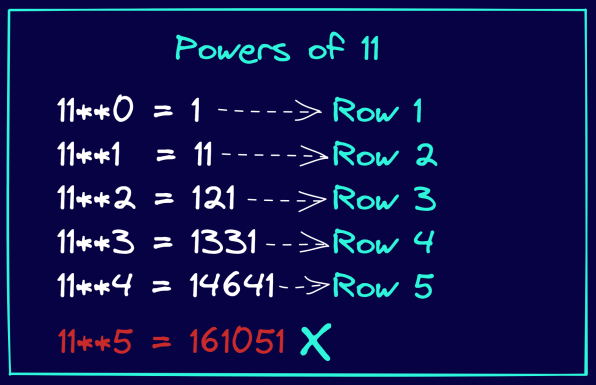
And when the number of rows you gotta print is at most 5you can use a straightforward technique.
Go through the figure below.
And observe how the powers of 11 are identical to the entries in Pascals triangle.
Also, notice that this works only up to the 4th power of 11.
As another example, call the functionpascal_triwith 4 as the argument.